Inteligência em grãos de areia

Download

Suponhamos que a Esfínge egípcia tenha um novo enigma, mais contemporâneo, baseado nas conquistas científicas e tecnológicas recentes da humanidade. Assim sendo, ela poderia questionar: “O que existe em comum entre as peças enfileiradas de um dominó, as bolas de uma de bilhar e um punhado de areia caindo de sua mão em um tabuleiro de xadrez?”

Segundo a mitologia, o custo de não saber a resposta correta de um enigma proposto pela Esfinge é o de ser engolido por ela. Porém, responder corretamente também significa saber que a resposta desse enigma envolveu o esforço e mesmo a vida de cientistas brilhantes e seus sacrifícios em períodos conturbados, como a Segunda Guerra Mundial, e também o investimento (de guerra e de reconstrução) das sociedades e instituições do último século. O MIT entre essas instituições.

O interessante é que a resposta deste “enigma” continua sendo um dos ramos de conhecimento e pesquisa mais intrigantes e prósperos da humanidade e integra duas áreas de conhecimento recentes: a ciência da computação e a teoria da complexidade. E este artigo explora essas relações, afinal, mais empolgante do que o enigma em si é explorar a sua resposta.

A Máquina de Turing

A ciência da computação moderna como a conhecemos tem início com Alan Turing em suas pesquisas pioneiras para identificar um computador universal, ou seja, definir as regras mínimas da computação nas quais todos computadores, sem exceção, precisam obedecer para serem completos.

Turing é muito popular pelos filmes de Hollywood como o cientista que desvendou a criptografia das máquinas nazistas Enigma, na Segunda Guerra, permitindo que os aliados interceptassem e decodificassem mais de 30 mil mensagens alemãs por mês, dando supremacia aos Aliados no Atlântico Norte e, consequentemente, reduzindo o conflito em pelo menos em dois anos, um feito por si só sobre-humano. Porém, sua verdadeira grande contribuição foi elaborar os fundamentos da computação moderna, por meio dos quais:

1) criou o modelo fundamental da computação;

2) mostrou que esse modelo (máquina de Turing) é universal por permitir processar qualquer problema computável;

3) demonstrou o que pode ou não ser computável.

Esse modelo fundamental nos permite afirmar que uma máquina de Turing é aquela que consegue transmitir sinais (informação) e mudar o estado desses mesmos sinais, que computacionalmente podem ser convertidos para ações moleculares e fundamentais como iniciar, mover, parar e sair (no caso da transmissão de um sinal) e ler e escrever (para a mudança de estado de um sinal armazenado).

O armazenamento deve ser suficiente o bastante para o processamento encerrar com sucesso, logo memória suficiente é parte fundamental da completude computacional. Ou seja, memória suficiente e as ações fundamentais de mover, ler e escrever um dado (ou sinal) podem ser consideradas as unidades fundamentais em qualquer computação.

A partir dos conceitos acima, em 1936, Turing escreveu um clássico da ciência, o artigo “Números Computáveis, aplicados ao Problema de Decisão (ou ENTSCHEIDUNGSPROBLEM)”. Neste artigo Turing idealizou teoricamente uma máquina mecânica  que lê uma fita com uma série de células sequenciais, como uma linha de uma tabela da planilha Excel, que serviria como memória e em cima dessa fita um cursor mecânico (header) capaz de ler e sobrescrever o conteúdo de cada uma dessas células e assim mover-se sobre a fita de acordo com algumas regras simples com as instruções condicionais da máquina de estado (mover, parar, sair, ler e escrever), como mostra a fig. 1:

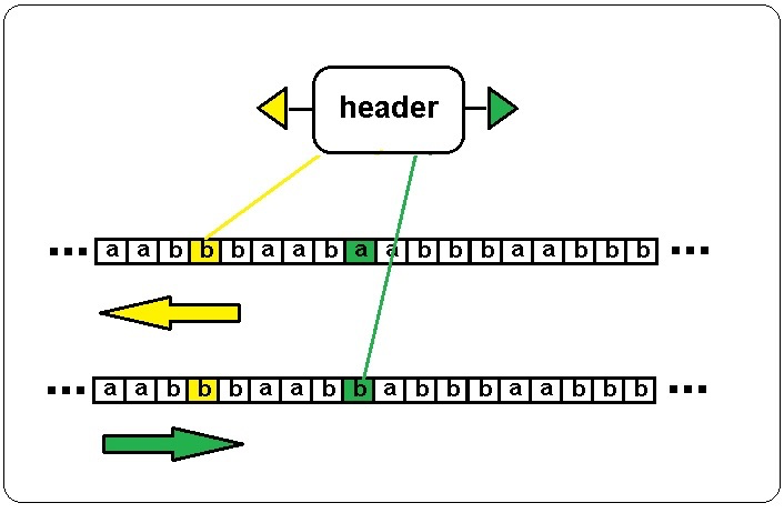
Fig 1 – Máquina de Turing

Na figura 1 o header se desloca inicialmente na fita de memória da direita para esquerda, lê o registro em amarelo e mantém a informação. Em seguida é enviado um segundo sinal (verde) para mover o header da esquerda para a direita e alterar o valor do registo de a para b. Em suma, este é o mínimo que todo computador deve obedecer para ser completo.

Essa descoberta, sem dúvida, teve impacto maior no mundo moderno do que a descoberta dos códigos da máquina Enigma, pois abriu precedente para um mundo de infindáveis artefatos que podem ser possíveis candidatos a máquinas ou modelos universais de Turing, desde que, claro, obedeçam às leis fundamentais de transmissão de sinais e manipulação e armazenamento desses mesmos sinais.

Atualmente, com os computadores presentes em praticamente todas atividades humanas modernas, a máquina de Turing pode ser vista como algo óbvio, porém não devemos nos enganar por esta simplicidade, pois na época em que Turing propôs este modelo os computadores não eram difundidos massivamente como hoje e para os que podem vir a contestar a genialidade de Turing, com base nesse modelo ele comprovou o que pode e o que não pode ser computável.

Para alcançar o feito histórico Turing utiliza com primazia o conceito de prova por contradição com técnica de computação chamada recursão para resolver o problema de decisão de David Hilbert (também conhecido como Entscheidungsproblem).  O que Turing fez foi assumir como premissa um computador capaz de responder com certeza se um programa, seja qual for, vai entrar em loop ou vai sair do loop (“halt”), conforme mostra a figura 2.

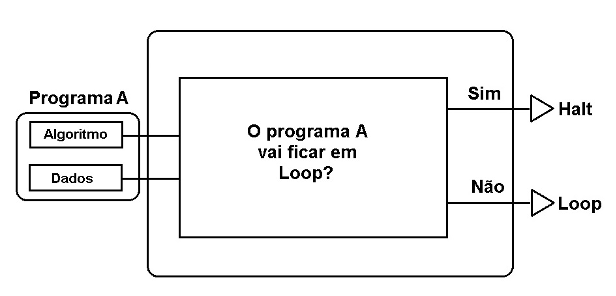
Fig 2 – Máquina capaz de decidir se um programa vai ficar em loop ou sair do loop (“halt”).

A máquina ou programa da figura 2 após identificar que o programa A recebido como entrada vai sair na execução (ou seja um “halt”) e não ficar em loop, ele responde Não e em seguida Turing adicionou mais uma informação inversa, que diz toda vez que a resposta recebida for a de confirmação de halt a máquina informará como sendo um loop (e vice-versa).

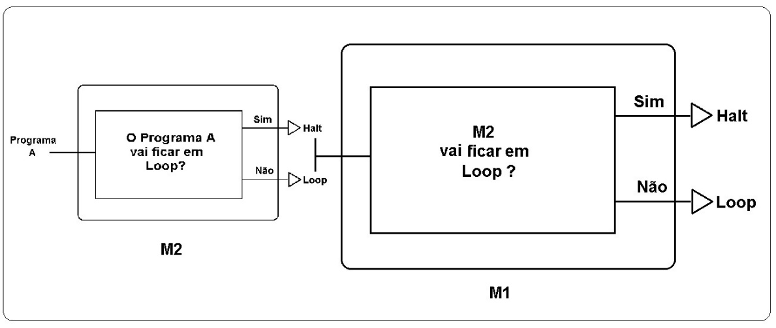
Fig 3 – A máquina que responde ao “Halting Problem” é usada como parâmetro dela mesma.

A genialidade da solução para o problema é que Turing assume a própria máquina da Figura 2 (M1) como entrada recursiva (M2) , como mostra a figura 3, pois ao incluir a máquina M1 como entrada recursiva (M2)  dela mesma é criada uma contradição à premissa, que diz ser possível informar se um programa vai ou não ficar em loop. O que invalida a premissa.

Essa contradição fica evidente por exemplo se M2 identifica que o Programa A entra em “Halt”, caso isso ocorra a resposta de M1 ao processar M2 entra em contradição pois informará que o programa A está em “Loop”, invalidando assim a premissa de que é possível existir um computador capaz de resolver o Problema de Decisão ou Halting Problema. Turing com esse exercício matemático e computacional simplesmente definiu que o escopo de processamento (e simulação) dos computadores é limitado e incapaz de simular, resolver ou prever todos os problemas.

Autômatos Celulares

Analisando a máquina de Turing com mais detalhes pode-se perceber, que cada quadrado da fita com os dados pode ser considerado uma célula e a própria máquina de Turing seria de forma abstrata uma ação programada ou automatizada em cima das células enfileiradas. Ou seja, a máquina de Turing é um autômato celular. Esse é um conceito poderoso que abre precedente para uma nova interpretação de mundo e uma nova ciência, o estudo dos Autômatos Celulares.

Com o avanço da pesquisa em computação percebe-se a importância dos Autômatos Celulares para modelagem de novas arquiteturas computacionais, assim como a simulação e interpretação de eventos não-lineares do mundo natural como estruturas de auto-organização e emergenciais.

John von Neumman é um dos primeiros a destacar a importância dos autômatos celulares em seus estudos de estruturas auto-replicantes, nos quais demonstrou a possibilidade de apresentarem comportamento semelhante a estruturas genéticas do mundo natural. Dois exemplos mais populares de Autômatos Celulares são os de uma única dimensão, de Wolfram, e o jogo da vida de John Conway.

Os autômatos de uma dimensão de Wolfram são um bom exemplo de como a simplicidade de regras podem gerar padrões complexos, pois a partir de um grid de uma dimensão idênticos ao da fita de memória da máquina de Turing da figura 1 aplica-se uma regra diferente das executadas pelo Header. No caso do Autômato de Wolfram, após a leitura de cada célula é criada uma nova linha (ou geração) baseada em uma regra e nas células vizinhas.

Por exemplo, se o conteúdo de uma determinada  célula da primeira geração é igual a 1 e da célula anterior é 0 e da posterior 0, é verificado a regra para gerar o novo número da nova geração da célula, conforme mostra a figura 4, neste caso para o valor 010 a regra informa que o valor da célula da próxima geração é igual a 0:

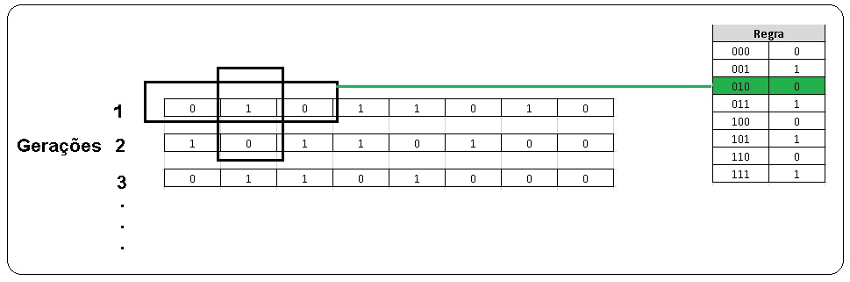
Fig 4 – Autômato de Wolfram.

Assumindo os zeros e uns como ligados e desligados de acordo com cada regra é gerado um padrão que para algumas regras específicas obedecem a princípios complexos como estruturas fractais. A figura 5 mostra alguns exemplos desses padrões formados por este autômata:

Fig 5 – Imagens geradas pelo autômato celular de Wolfram conforme regras pré-definidas.

Fonte: https://mathworld.wolfram.com/Rule110.html

Outro autômato celular conhecido é o jogo da vida criado pelo matemático John Conway. Este, ao contrário da Máquina de Turing e do Autômato de Wolfram, ambos de uma dimensão (com uma única fila de células), tem duas dimensões (no caso um grid ou um tabuleiro de xadrex). Assim como no modelo de Wolfram, as regras são baseadas na vizinhança e duas regras simples, no caso:

• uma célula permanece ligada na próxima geração se tiver dois ou três vizinhos ligados entre as oito células com as quais faz vizinhança, caso contrário é desligada;
• uma célula apagada torna-se ligada na próxima geração se tiver três vizinhos ligados.

Essas duas regras simples com o decorrer do processamento e de acordo com as condições iniciais, a cada nova geração criam uma variedade de estruturas auto-organizadas, de osciladores estáveis a estruturas voadoras como gliders.

Não menos importante, é o fato que a regra de número 110 do Autômato de Wolfram e o jogo da vida de Conway são máquinas de Turing completas.

Mas como isso é possível que os autômatos de Wolfram e Conway tenham completude computacional?

Como vimos, a máquina de Turing é essencialmente um mecanismo capaz de processar um sinal, e a regra 110 do Autômato de Wolfram e o jogo da vida de Conway, por mais incrível que pareça, geram padrões capazes de enviar sinais e permitem processá-los. Um dos casos mais especiais são as estruturas auto-organizadas criadas pelo Jogo da Vida, capazes de emitir um sinal, chamados de Glider Guns, que podem ser processados por portas lógicas criadas com estruturas auto-organizadas do próprio jogo da Vida.

Podemos estrapolar a aplicação de autômatos celulares para cenários mais variados e cotidianos, por exemplo se assumirmos um tabuleiro de xadrez ou uma mesa de jantar e dividi-la em uma grid com várias células, e nesse caso também é teoricamente possível criar um computador ou uma máquina completa de Turing, desde que obedeçam a algumas regras, quando estiverem caindo de nossas mãos no tabuleiro.

Vamos supor que sejamos capazes de desenvolver um mecanismo no qual cada célula presente na mesa seja capaz de contar os grãos de areia que caem em cima delas mesmas e em seguida também sejam capazes de distribuir o excesso de grãos para outras células. Determinamos as seguintes regras abaixo para o autômato de grãos de areia:

• toda célula na mesa do tabuleiro pode ter no máximo 3 grãos de areia;
• se uma célula tiver mais de 3 grãos, o excesso deve ser distribuído entre as células adjacentes até que não tenha mais grão nenhum na célula.

E, de novo, por mais surpreendente que pareça, este modelo chamado de SandPile model, também passa no teste de completude de Turing.

Mas como?

A resposta é a capacidade do modelo de transmitir sinais e processá-los com as estruturas auto-organizadas que vão sendo criadas conforme as regras e condições aplicadas. Por exemplo, uma série de células com quatro grãos de areia fica em um estado de instabilidade que gera reações em cadeia que podem ser utilizadas para modelar a transmissão do sinal. Fica cada vez mais óbvia a resposta para a questão do início do artigo, pois o potencial de computação de praticamente tudo que nos cerca é impressionante, sendo possível criar um computador com praticamente tudo, seja criando portas lógicas com o uso de dominós enfileirados ou mesmo com a colisão de bolas de bilhar, exemplo este inclusive que tem sido utilizado para modelar novos tipos de portas lógicas (Portas lógicas de Fredkin) e novos modelos computacionais tradicionais e de computadores quânticos.

Adianto, porém, que existe algo mais profundo sobre esse tema. E o mais famoso cientista da Ciência de Computação do MIT quem nos apresentou a primeira pista para essa visão mais holística sobre o alto potencial de computação do universo em que vivemos.

Entropia da Informação

Sempre me questiono qual foi o maior cientista de todos os tempos do MIT, e pessoalmente entendo que o embate está entre Noam Chomsky, Richard Feynman e Claude Shannon. Mas se a competição for decidida pelo número de estátuas no Campus, cabe a Shannon a vitória. Brincadeira a parte, Shannon, ao lado de Turing e John von Neumman, são considerados justamente os pais fundadores da Ciência da Computação Moderna.

Um ponto crucial para a computação, é a transmissão do sinal, como vimos na máquina de Turing representada essencialmente pelas ações de iniciar, mover, parar e sair. A descoberta fundamental de Shannon foi identificar as leis da Teoria da Informação, em especial as que regem a transmissão de sinais ou dados, no caso a definição de entropia.

A entropia é a medida do grau de incerteza ou de variação da informação transmitida, por exemplo, considerando duas mensagens diferentes a serem transmitidas digitalmente, onde uma primeira mensagem é formada pelos sinais digitais gerados com base no resultado do lançamento de uma moeda (Zero para cara e Um para Coroa) e a segunda mensagem é uma música (também convertida digitalmente).

Segundo Shannon a primeira mensagem do exemplo é a que possui a maior entropia possível, por possuir um maior grau de incerteza para o receptor, enquanto que a segunda mensagem, por possuir um grau de incerteza menor para o receptor da mensagem possui uma entropia menor, consideravelmente menor.

O rigor das pesquisas de Claude Shannon, leva a conclusões importantes não somente para a Ciência da Computação, mas para a Ciência como um todo, pois fica evidente a relação direta entre entropia na Teoria da Informação e na termodinâmica. Esta última mede, por exemplo, o grau de desordem da matéria, enquanto na teoria da informação o grau de incerteza na transmissão da informação, dois temas diretamente relacionados.

Não menos impressionante também é identificação da relação direta entre os estudos probabilísticos de Shannon com a compressão de dados e com os fundamentos da teoria quântica moderna. É por esse motivo que muitos consideram o artigo de Shannon chamado “A origem matemática da Teoria da Comunicação” como um dos mais importantes artigos da Ciência.

As medidas de entropia na transmissão da informação, também são chamados de graus de inteligência na transmissão, uma vez que é factível afirmar que transmissões com conhecimento envolvem entropias específicas bem diferenciadas do ruído de sinal gerado pelo resultado do lançamento de moedas, o que permite a liberdade para supormos que o alto índice de computabilidade do universo esteja associado a sua natureza discreta e não a uma natureza contínua.

 A resposta da Esfinge

O que existe em comum entre as peças enfileiradas de um dominó, as bolas de uma mesa de bilhar e um punhado de areia caindo de sua mão em um tabuleiro de xadrez é que todos estes podem criar computadores completos.

Mas essa é a resposta certa para o nosso nível de conhecimento atual, pode ser que a Esfinge com toda sua sabedoria diga: “Errado. A resposta é o segredo da vida.” Se ela fizer isso, você terá sido engolido, claro. Mas antes dela te engolir, dará a explicação: “O mundo é um autômato celular e a inteligência está em grãos de areia.”

Uma interpretação para essa resposta final da esfinge vem do fato de ser possível criar computação com praticamente tudo o que nos cerca, e uma forte tendência para um universo ser formado por sinais discretos ou pacotes. Isso tem implicação na origem da vida, o que seria uma conclusão radical para a pergunta do início do artigo, pois, como vimos, autômatos celulares são capazes de gerar estruturas auto-organizadas complexas a partir de regras muito simples e cuja medida de inteligência, como comprovou Shannon, pode ser avaliada por graus específicos de entropia na transmissão da informação.

Logo, nada impede que os raios de sol no passado (e talvez ainda hoje), em especial a radiação ultravioleta, em uma determinada entropia contenham as regras dos autômatos celulares iniciais que geraram a vida na terra, no caso as moléculas de aminoácidos.

Quem sabe se monitorarmos o Sol por determinados padrões entrópicos nas mensagens dos raios solares, conseguimos ainda encontrar uma mensagem primordial que pode ter despertado as primeiras estruturas autômatas na Terra e, assim sendo, identificando talvez um padrão capaz de gerar vida não somente aqui, mas em outros planetas também?

Homenagem

Foi no período conturbado da Segunda Guerra que Alan Turing, John Von Neumann e Claude Shannon, cientistas dos países aliados e pais fundadores da Computação Moderna, produziram os artigos considerados entre os mais valiosos de toda a nossa história da Ciência Moderna, e com suas ideais e pesquisas científicas nos ofereceram uma nova visão de mundo.

Se parte da população mundial consegue hoje trabalhar de casa em seus computadores, protegidos da pandemia, é resultado, em parte, do esforço, conquistas e lutas dos grandes cientistas citados neste artigo. Cada um sofreu e lutou contra todo tipo de adversidade, para oferecer o seu melhor, seja Turing lutando contra o preconceito com a sua sexualidade, Von Neumman na sua luta contra os terríveis efeitos da radiação que recebeu no Projeto Manhattan ou Shannon em sua luta contra o Alzheimer.

Por mais que a indústria da computação seja uma consequência das necessidades dos mercados e das disputas competitivas (e conflitos) entre empresas e nações, não é possível negar a importância fundamental de alguns poucos homens e mulheres no destino e nos caminhos trilhados pela indústria da computação em particular. Esse artigo é uma homenagem aos profissionais desta área e em especial aos pais fundadores da computação moderna, pois se hoje desfrutamos os benefícios que a Ciência da Computação nos traz, isso não veio de graça, mas sim do alto custo de muitas vidas em especial dos países aliados na Segunda Guerra Mundial, entre eles o Brasil.  A eles o nosso sincero agradecimento.