
A matemática há muito representa um abrigo contra a confusão e a dúvida, um lugar aonde vamos à procura de respostas. Parte dessa mística talvez decorra do fato de que as biografias de matemáticos frequentemente os retratam como sábios de outro mundo – pessoas que parecem extrair do nada as verdades profundas da natureza e as transcrevem em uma prosa tão sucinta e confiante que deve ser lida de forma meditativa, uma palavra de cada vez. Como estudante de pós-graduação em física, sei o trabalho que dá conduzir experimentos delicados, mas a rotina diária das descobertas matemáticas é um ritual totalmente desconhecido para mim. E esse sentimento é reforçado ainda mais por livros populares de matemática, que muitas vezes adotam o tom de um pastor em pregação aos fiéis.
Em física, as perguntas que fazemos e teorias que criamos têm por objetivo explicar melhor a realidade subjacente. Na verdade, alguns conceitos – como o fato de que cargas opostas se atraem, ou de que a desordem ou entropia tende a aumentar – são tão universalmente arraigados em nossa experiência que se infiltram na linguagem cotidiana como metáforas. Volta e meia me pego recorrendo a vocabulário de pesquisa e analogias da física para dar explicações. Mas, apesar de ter estado próximo à matemática pela maior parte de minha vida, continuo perplexo com a pesquisa matemática. O que a motiva e qual é o seu objetivo final? Como uma pessoa imersa na cultura da matemática vê o mundo? Então, quando descobri que Terence Tao, lenda viva da matemática contemporânea, estava oferecendo uma aula online sobre sua abordagem do “pensamento matemático”, tive que dar uma olhada.
O curso, com duração de filme, distribuído pela MasterClass, começa de forma bastante convidativa. Tao emana calma e confiança. Uma mentalidade matemática, diz ele, torna “o mundo complexo um pouco mais administrável”. Ele sugere que sua aula pode ser “ainda mais adequada àqueles que não tem treinamento formal em matemática”. Mas, em pouco tempo, a futilidade da sua tentativa de desmistificar a matemática se torna inevitável.
Pela maior parte da sessão, Tao fica sentado em uma poltrona branca; não há quadros, nem canetas, nem papéis. “A matemática é uma linguagem de comunicação precisa”, diz Tao. Ainda assim, nessa aula, ele não faz uso das ferramentas mais poderosas para alcançar esse fim. Embora ele tente ser acessível, falando sobre como certa vez foi mal em uma prova e sobre suas dificuldades para instalar cortinas, eu não me senti mais próximo do mundo da matemática. Após 90 minutos assistindo, as conclusões que me restaram eram indistinguíveis daquilo que eu poderia aprender em um retiro espiritual: “Tudo está conectado” e “Abrace o fracasso”.
Eu não sou o único que tentou – e não conseguiu – entrar para a igreja da matemática. Recentemente, Alec Wilkinson, escritor para o jornal The New Yorker e adepto de longa data do auto-aperfeiçoamento, embarcou em um projeto de um ano para dominar um pouco da matemática básica que não compreendia em sua juventude: álgebra, geometria e cálculo. Em seu livro de 2022, A Divine Language (em tradução livre, Uma Linguagem Divina), ele descreve sua jornada como busca por redenção após a luta contra a matemática de nível médio. “Ela havia me maltratado e eu me sentia insultado”, escreveu ele. “Eu estava voltando, com meio século de sabedoria, para tirar o sorriso da cara da matemática.”
Wilkinson tem um plano melhor que o meu: ele começa com livros didáticos padrão. E tem ajuda. Sua sobrinha, professora de matemática, concordou em acompanhá-lo nessa jornada. Mas até mesmo os primeiros passos na álgebra são árduos. O ceticismo dos adultos atrapalha; ele não consegue aceitar as regras – a forma como variáveis podem ser somadas e multiplicadas, como frações e exponentes funcionam – tão prontamente quanto uma criança. E mais, acha a redação dos livros didáticos atroz.
Revisitar a álgebra quando adulto, declara Wilkinson, é “como encontrar alguém que você não vê há anos e se lembrar de por que nunca gostou dele ou dela”.
“Há uma certa arrogância na prosa, como se aprender matemática não só fosse divertido! mas também obscuramente patriótico, o dever do adolescente enquanto cidadão em formação”, escreve ele. “Além de omitir coisas, eles eram descuidados quanto à linguagem, suas frases eram bagunçadas, seu pensamento frequentemente desleixado e o tom muitas vezes alegre e irracionalmente impaciente.” Embora ele enfrente a álgebra com um rigor determinado, durante seis horas por dia, seis a sete dias por semana, e fique obcecado por ela o restante do tempo, a simples competência continua a lhe escapar. Revisitar a álgebra quando adulto, declara ele, é “como encontrar alguém que você não vê há anos e se lembrar de por que nunca gostou dele ou dela”.
Quando Wilkinson não está debruçado sobre livros didáticos, fica deslumbrado com misticismo que cerca a matemática. Os matemáticos com quem conversa falam de sua profissão com sentimentos quase religiosos e pensam em si mesmos como meros prospectores de uma ordem transcendental. Quando Wilkinson reclama com sua sobrinha que a matemática não se deixa dominar, ela diz: “Por um momento, pense nela como uma disciplina monástica. Você tem que ter fé no que eu te digo.” Onde sua sobrinha e outros veem padrões e ordem, ele percebe somente “incoerência, obscuridade e caos” e se sente como um monge que vê menos anjos que todos ao seu redor. Ele agora recrimina sua educação e o seu “eu” mais jovem: Por que não aprendeu melhor tudo isso quando tinha a impressionabilidade de uma criança?
Um ano depois, Wilkinson consegue resolver alguns problemas de cálculo, mas a jornada foi difícil, o terreno acidentado e, muitas vezes, hostil. Frequentemente se fala da matemática como uma linguagem que tem a lógica como sua gramática. Mas quando você estuda uma língua como o Espanhol, você pode aprender algumas palavras e imediatamente desvendar uma nova cultura. Os passos introdutórios à matemática formal, por outro lado, demandam um compromisso com o rigor e com a abstração, sem oferecer qualquer utilidade. Entre os matemáticos, descobriu Wilkinson, existe até um certo escárnio em relação àqueles que buscam aplicações úteis. Nesse sentido, a famosa frase de G.H. Hardy, de 1940: “Mas a situação do estudioso comum da matemática aplicada não é um pouco patética?” Ou, mais recentemente, o comentário de John Baez: “Se você não gosta de abstração, por que trabalhar com matemática? Talvez você devesse trabalhar na área de finanças, onde todos os números vêm com cifrões na frente.” A única promessa da matemática, em troca de lealdade inabalável, é a de um plano superior, bem como acontece em um culto. Wilkinson acabou tão atordoado e exausto quanto uma vítima de naufrágio ilhada no Ártico.
Minhas frustrações e as de Wilkinson ressaltam as inadequações dos meios geralmente empregados para o ensino da matemática. Livros didáticos nem sempre são escritos tendo a acessibilidade em mente. Eles oscilam entre o pedantismo e a indiferença, e os exercícios que apresentam podem parecer uma série atividades inúteis. Ao mesmo tempo, tentativas de esquematizar o assunto podem ser frustrantes. Wilkinson e eu realmente precisávamos de uma voz solidária; do testemunho de alguém que já chegou ao ápice da matemática abstrata, mas também tem a paciência para guiar um iniciante.
A matemática e pianista Eugenia Cheng foi o mais próximo que cheguei de encontrar essa voz.
Eu me interessei pelos livros de Chang porque compartilho de sua paixão por cozinhar. Para a feliz proprietária de uma batedeira e de diversos pincéis de massa, o título Cakes, Custard and Category Theory (em tradução livre, Bolos, Creme e a Teoria das Categorias) soava delicioso de mais para deixar passar. Seu primeiro capítulo, sobre a natureza epistêmica da matemática, começa com uma receita de brownie. Cheng diz que tropeçar em novas ideias matemáticas é como errar tanto em uma receita de suflê que, no final, o resultado são biscoitos. Eu fui facilmente fisgado.
Muitos livros populares sobre matemática tentam ser acessíveis falando sobre mercado de ações ou jogos de pôquer. Outros tratam de forma poética os números primos e o mistério do infinito. Os livros de Cheng elevam os leitores às alturas rarefeitas da abstração matemática ensinando teoria das categorias, a qual ela acredita ser o tipo mais fundamental de matemática.
A teoria das categorias pode parecer esotérica, mas é a gramática subjacente à lógica matemática. Os livros de Cheng abrem as cortinas para mostrar como pesquisas matemáticas podem ser banais; o ato de transformar um axioma inviolável em argumentos complexos é apenas o equivalente acadêmico de construir uma espaçonave de Lego com pecinhas indestrutíveis. Mas o mais importante é que esses livros nos convidam a mudar nossa visão de mundo, a simplificar o pensamento em abstrações, a interpretar e analisar o mundo em termos matemáticos.

Lendo Cakes, Custard and Category Theory (também publicado como How to Bake Pi), rapidamente descobrimos que as sobremesas são apenas uma estratégia. Cada capítulo começa com uma receita, seguida de uma analogia entre matemática e cozinhar. A massa folhada serve como lembrete de que precisão extrema é parte da pesquisa matemática; em outro momento, aprendemos que não há um jeito certo de fazer bolo e que devemos ser flexíveis quanto aos ingredientes e à técnica. Essas analogias podem parecer superficiais e até forçadas. Mas, felizmente, elas logo abrem espaço para uma conversa casual sobre tópicos matemáticos.
Cheng entende que o vocabulário firme da lógica pode ajudar pessoas envolvidas em discussões acirradas a perceber que as diferenças entre elas não são tão irreconciliáveis.
O livro mais recente de Cheng, The Joy of Abstraction (em tradução livre, A Alegria da Abstração), trata dos mesmos temas, mas se parece mais com um livro didático de graduação. Seus capítulos, com títulos como, “Isomorfismo” e “Functores”, fornecem uma introdução relativamente rigorosa à teoria das categorias e são repletos de teoremas, provas e exercícios. Ocasionalmente, Cheng faz digressões sobre como certos conceitos têm paralelos etimológicos e semânticos na vida real – uma “função” pode ser pensada como uma máquina de venda automática, um “conjunto” pode representar um grupo de pessoas (e podemos dividir esse conjunto em “partições” ou “amizades”). Mas tendo montado o cenário com objetos familiares, ela rapidamente começa o trabalho duro de manipulá-los usando lógica. Em suma, seus livros são uma introdução humana aos fundamentos da matemática e dão um bom panorama do que os matemáticos passam seu tempo refletindo.
Existe um aspecto, contudo, no qual seus livros de matemática se diferenciam acentuadamente de livros didáticos de graduação. Um tema recorrente na escrita de Cheng é o de que o mundo é mais bem compreendido quando em forma simplificada, e de que noções de matemática abstrata são capazes até de fomentar a empatia e o senso de justiça. Amigos que tentam ser solidários em um momento de mágoa e ficam perguntando sobre os detalhes dolorosos deveriam se contentar em saber apenas que (a) você amava alguma coisa e (b) que você perdeu essa coisa recentemente. É simples assim; todos os outros detalhes são supérfluos.

O argumento mais heterodoxo de Cheng – melhor apresentando em seu livro A Arte da Lógica num Mundo Ilógico – é o de que a teoria das categorias pode, na verdade, ser empregada em nossa vida cotidiana, tornando discussões sobre privilégios, assédio sexual, racismo e até fake News, menos controvertidas. Por exemplo, ela acha que o debate sobre seguridade social pode ser descrito em termos de “falsos positivos” e “falsos negativos”: “Um falso negativo, nesse caso, seria alguém que merece auxílio, mas não recebe; um falso positivo seria alguém que não merece auxílio, mas recebe.” O debate, argumenta ela, não é sobre se devemos ajudar as pessoas (claro que devemos!), mas sobre até que ponto devemos relevar esses falsos positivos e negativos. Alguém que deseje reduzir a quantidade de dinheiro gasta com seguridade social provavelmente se incomoda com a ideia de que falsos positivos abusam do sistema, recebendo benefícios que não merecem. Cheng entende que o vocabulário firme da lógica pode ajudar pessoas envolvidas em discussões acirradas a perceber que as diferenças entre elas não são tão irreconciliáveis (afinal, ambos querem ajudar as pessoas) e encaminhá-las para uma conversa mais aprofundada sobre “até que ponto” e “em que circunstâncias”.
Cheng acredita que podemos encorajar a empatia por meio de analogias logicamente relacionadas. Inicialmente perplexa com homens que protestam contra graves acusações de privilégio ou agressão, ela acha útil comparar esses protestos à sua exasperação quando pessoas se ressentem dos graduados em escolas de elite (como ela mesma) por terem o sucesso garantido por seus pais, embora ela tenha tido que trabalhado duro. Dizem que isso a tornou mais empática em relação aos homens: emoções se intensificam justificadamente quando experiências individuais contrastam com as generalizações de um grupo.
Entretanto, a aplicação desses argumentos a casos mais complexos parece cada vez mais suspeita. Um diagrama que aparece em muitos dos livros de Cheng é o “cubo do privilégio”. Em um canto do cubo está o conjunto vazio {}. A partir desse canto (inferior anterior esquerdo na ilustração), você pode seguir em três direções para chegar a um dos três tipos de privilégio: branco, homem e rico. Se você seguir em todas as três direções, uma após a outra, você chega ao canto oposto, com todos os privilégios {branco, homem, rico}.
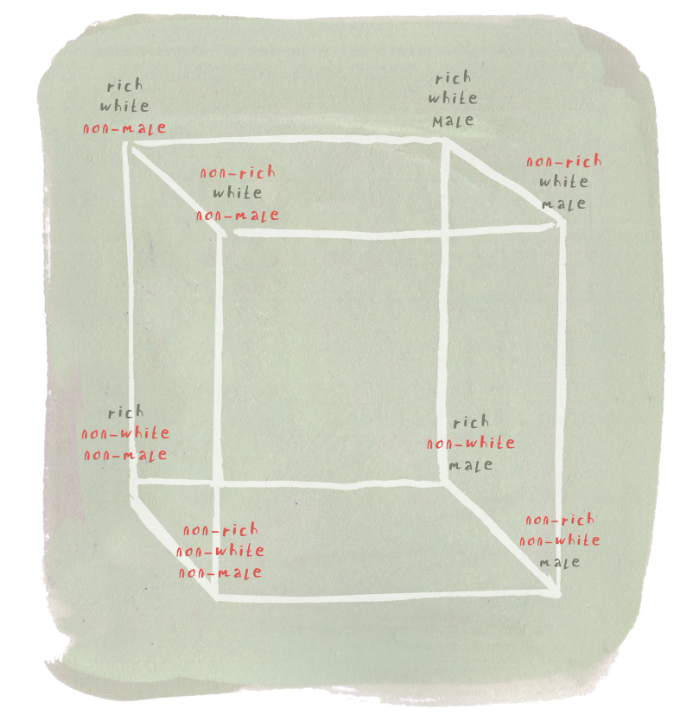
Cheng ilustra a ideia de interseccionalidade com representações como essa, retratando privilégios em múltiplas dimensões.
JENNY KROIK
Para teóricos das categorias, essa é a descrição mais sucinta de interseccionalidade: a ideia de que atributos como classe, gênero e raça podem interagir para produzir manifestações complexas de desigualdade. O diagrama de Cheng mostra como combinações de privilégios em múltiplas dimensões podem formar hierarquias complicadas, de modo que pessoas com três tipos de privilégio estão necessariamente em uma situação melhor do que pessoas com apenas dois tipos. Mas quando Cheng usa esse diagrama para adentrar questões mais espinhosas, como por que “um homem branco que não cresceu rico” pode se sentir particularmente ofendido por um homem não branco que seja mais rico e tenha uma situação melhor, sua resposta é insatisfatória: no cubo do privilégio “não há uma linha entre homem rico não branco e homem branco não rico (os dois grupos habitam cantos desconectados de uma diagonal), então a teoria do privilégio não diz nada sobre a situação relativa desses dois grupos”. A desculpa pode até ser logicamente consistente, mas certamente não é o tiro de misericórdia retórico que esperamos aprender após nos engajarmos em raciocínio abstrato por vária semanas.
Podemos equipar as pessoas com ferramentas rigorosas para evitar escorregões e ambiguidades na linguagem cotidiana, mas essas ferramentas nem sempre vêm com diretrizes éticas. O pânico Malthusiano quanto à explosão populacional, por exemplo, emergiu de observações sobre funções exponenciais e vem sendo usado para justificar políticas anti-imigração, bem como genocídios. Modelos de computador matematicamente inspirados são rotineiramente provados tendenciosos. Um livro altamente controverso de 1994 escondeu seus esforços dúbios para conectar raça e inteligência por trás do título matemático The Bell Curve (A Curva de Sino). A exemplo da Bíblia, do livro A Democracia na América, de Tocqueville, e outros títulos renomados, a literatura matemática é vasta o bastante para justificar e reforçar qualquer tipo de pensamento, ainda que impopular, problemático ou tolo.
Mesmo assim, ainda há um sentido em que a missão de Eugenia Cheng de desmistificar a matemática é extremamente nobre. Seus livros tentam replicar o ritual monótono de construir argumentos a partir de provas incontestáveis e, o mais importante, mostram como uma visão de mundo inspirada pela matemática poderia ser, tanto em sua estranheza como em sua permissividade. Você pode achar essas visões de mundo odiosas e desagradáveis, mas a lição principal dos livros de Cheng é a de que comunicar um pensamento complexo de uma mente para outra, para não falar entre culturas e linguagens, não é tarefa fácil. Aprimorar a arte de expressar ideias de forma caridosa e clara é algo de que todos nos beneficiaríamos.
O que eu acho mais inspirador na cultura da matemática é como ela vem resistindo ao tempo, seguindo uma mesma linha em diferentes civilizações. A matemática conseguiu unificar descobertas díspares pelo mundo todo e há enigmas elaborados séculos atrás ainda sendo ponderados. Uma das razões pelas quais essa cultura pode parecer desconcertante para um iniciante é que a matemática contemporânea reduziu ideias de milênios, antes ricas e vívidas, a símbolos lacônicos e terminologias esotéricas que nem sempre são fáceis de dominar. Livros populares de matemática buscam uma visão mais original dessas velhas ideias, seja por meio de receitas culinárias, seja por meio de questões políticas controvertidas. Meu veredito: Por que não? Vale a pena tentar.
Pradeep Niroula é doutorando em física em Washington, D.C.






