A não ser que você seja um físico ou engenheiro, realmente não há muitos motivos para você saber equações diferenciais parciais. Eu sei. Após anos estudando-as na graduação enquanto estudava engenharia mecânica, nunca mais as usei no mundo real.
Mas equações diferenciais parciais, ou EDPs, também são um pouco mágicas. Elas são uma categoria de equações matemáticas que são realmente boas para descrever mudanças no espaço e no tempo e, portanto, muito úteis para descrever os fenômenos físicos em nosso universo. Elas podem ser usadas para modelar tudo, desde órbitas planetárias e placas tectônicas até a turbulência do ar que perturba um voo, o que nos permite fazer coisas práticas como prever atividade sísmica e projetar aviões seguros.
O problema é que as EDPs são notoriamente difíceis de resolver. E aqui, o significado de “resolver” talvez seja melhor ilustrado por um exemplo. Digamos que você esteja tentando simular a turbulência do ar para testar um novo projeto de avião. Existe uma EDP conhecida chamada Navier-Stokes que é usada para descrever o movimento de qualquer fluido. “Resolver” a EDP Navier-Stokes permite captar o movimento do ar (também conhecido como condições do vento) em qualquer momento e modelar como ele continuará a se mover ou como estava se movendo antes.
Esses cálculos são altamente complexos e computacionalmente intensos, razão pela qual as disciplinas que usam muitas EDPs geralmente dependem de supercomputadores para fazer as contas. É também uma razão pela qual o campo da Inteligência Artificial (IA) tem tido um interesse particular por essas equações. Se pudéssemos usar a deep learning para acelerar o processo de resolvê-las, isso poderia ser muito bom para a investigação científica e a engenharia.
Agora, os pesquisadores do Instituto de Tecnologia da Califórnia (Caltech) apresentaram uma nova técnica de deep learning para resolver EDPs que é muito mais precisa do que os métodos desenvolvidos anteriormente. Também é muito mais generalizável, capaz de resolver famílias inteiras de EDPs – como a equação de Navier-Stokes para qualquer tipo de fluido – sem a necessidade de retreinamento. Além disso, é 1.000 vezes mais rápida do que as fórmulas matemáticas tradicionais, o que reduziria nossa dependência de supercomputadores e aumentaria nossa capacidade computacional para modelar problemas ainda maiores. É isso aí. Podem mandar ver.
Felicitações de MC Hammer
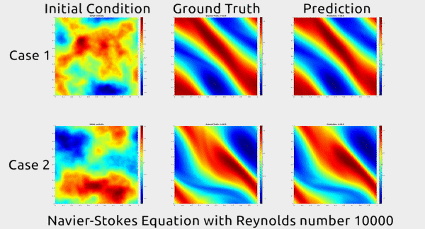
Antes de nos aprofundarmos em como os pesquisadores fizeram isso, vamos primeiro apreciar os resultados. No gif abaixo, você pode ver uma demonstração impressionante. A primeira coluna mostra dois instantâneos do movimento de um fluido; a segunda mostra como o fluido continuou a se mover na vida real; e a terceira mostra como a rede neural previu que o fluido se moveria. Ela basicamente parece idêntica a segunda.
O artigo ganhou muita atenção no Twitter, e até mesmo um elogio do rapper MC Hammer. Sim, de verdade.
Ok, de volta a como eles fizeram isso.
Quando a função se encaixa
A primeira coisa a se entender aqui é que as redes neurais são fundamentalmente aproximações de função. (É o quê?) Quando elas são treinadas em um conjunto de dados de entradas e saídas emparelhadas, elas estão, na verdade, calculando a função, ou a série de operações matemáticas, que irão transpor uma para a outra. Pense em construir um detector de gatos. Você está treinando a rede neural alimentando-a com muitas imagens de gatos e coisas que não são gatos (as entradas) e rotulando cada grupo com 1 ou 0, respectivamente (as saídas). A rede neural então procura a melhor função que pode converter cada imagem de um gato em 1 e cada imagem de todo o resto em 0. É assim que ela pode olhar para uma nova imagem e dizer se é ou não um gato. Ela está usando a função que encontrou para calcular sua resposta – e se seu treinamento foi bom, ela acertará na maioria das vezes.
Convenientemente, esse processo de aproximação de função é o que precisamos para resolver uma EDP. Em última instância, estamos tentando encontrar uma função que melhor descreva, digamos, o movimento das partículas de ar sobre o espaço físico e o tempo.
E é esse o ponto crucial do artigo. As redes neurais são geralmente treinadas para aproximar funções entre entradas e saídas definidas no espaço euclidiano, seu clássico gráfico com eixos x, y e z. Mas desta vez, os pesquisadores decidiram definir as entradas e saídas no espaço de Fourier, que é um tipo especial de gráfico para traçar frequências de ondas. A ideia deles, que foi baseada em trabalhos em outras áreas, é que algo como o movimento do ar pode realmente ser descrito como uma combinação de frequências de ondas, explica a professora Anima Anandkumar do Caltech, que supervisionou a pesquisa junto a seus colegas, professores Andrew Stuart e Kaushik Bhattacharya. A direção geral do vento em um nível macro é como uma baixa frequência com ondas muito longas e letárgicas, enquanto os pequenos redemoinhos que se formam no nível micro são como altas frequências com ondas muito curtas e rápidas.
Por que isso importa? Porque é muito mais fácil aproximar uma função de Fourier no espaço de Fourier do que resolver uma EDPs no espaço euclidiano, o que simplifica muito o trabalho da rede neural. Além disso, gera benefícios de grande precisão e eficiência graças a sua grande vantagem de velocidade sobre os métodos tradicionais: essa técnica tem uma taxa de erro 30% menor para resolver Navier-Stokes do que os métodos já conhecidos de deep learning.
Tudo isso é muito mais engenhoso e também torna o método mais generalizável. Os métodos anteriores de deep learning tiveram que ser treinados separadamente para cada tipo de fluido, enquanto este só precisa ser treinado uma vez para lidar com todos eles, conforme confirmado pelos experimentos dos pesquisadores. Embora eles ainda não tenham tentado estender isso a outros exemplos, ele também deve ser capaz de lidar com todas as composições da Terra ao resolver EDPs relacionadas à atividade sísmica, ou todo tipo de material ao resolver EDPs relacionadas à condutividade térmica.
Supersimulação
Os professores e seus alunos de doutorado não fizeram essa pesquisa apenas por diversão teórica. Eles querem levar IA para mais disciplinas científicas. Falando com vários colaboradores da ciência do clima, sismologia e ciência dos materiais, Anandkumar decidiu enfrentar o desafio das EDPs com seus colegas e alunos. Eles agora estão trabalhando para colocar seu método em prática com outros pesquisadores do Caltech e do Lawrence Berkeley National Laboratory.
Um tópico de pesquisa com o qual Anandkumar está particularmente animada: as mudanças climáticas. Navier-Stokes não é apenas bom em modelar turbulência do ar; também é usado para padrões climáticos. “Ter boas previsões meteorológicas refinadas em escala global é um problema tão desafiador”, diz ela, “e mesmo nos maiores supercomputadores, não podemos fazer isso em uma escala global hoje. Portanto, se pudermos usar esses métodos para acelerar todo o processo, isso seria tremendamente chocante”.
Existem também muitas, muitas outras aplicações, acrescenta ela. “Nesse sentido, o céu é o limite, já que temos uma forma geral de acelerar todas essas aplicações”.





